Cách chứng minh ba điểm thẳng hàng lớp 9
Chứng minh hai đoạn thẳng, tạo thành từ 3 điểm đã cho, cùng song song với một đường thẳng nào đó.
Bạn đang xem: Cách chứng minh ba điểm thẳng hàng lớp 9
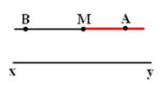
Chẳng hạn chứng minh :
AM//xy và BM//xy => A, M, B thẳng hàng ( tiên đề Ơclit ).
Phương pháp 3 : Sử dụng tính chất của hai đường thẳng vuông góc
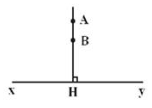
Chẳng hạn chứng minh :
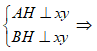
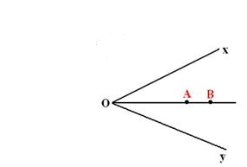
Chứng minh : + Tia OA và OB cùng là tia phân giác của $\widehat{xOy}$
+ Tia OB là tia phân giác của góc $\widehat{xOy}$
=>A , O , B thẳng hàng
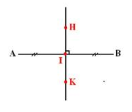
Chứng minh H , I , K cùng thuộc đường trung trực của AB
=>H , I , K thẳng hàng
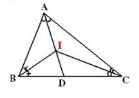
Chứng minh : +) I là trọng tâm của ∆ ABC
+) AD là trung tuyến của ∆ ABC
=>A , I , D thẳng hàng
+ ) Tương tự đối với ba đường cao , phân giác , trung trực trong tam giác.
II . Bài tập áp dụng :
Bài 1 : Cho tam giác ABC vuông tại A, M là trung điểm AC. Kẻ tia Cx vuông góc CA ( tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC ) . Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng .
Giải
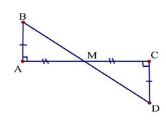
AB = CD ( đối đỉnh )
$\widehat{MAB}=\widehat{MCD}=90{}^\circ $
MA = MC ( M là trung điểm AC )
=>$\Delta AMB$= $\Delta CMD$ (c.g.c)
=>$\widehat{AMB}$=$\widehat{CMD}$ ( hai góc tương ứng )
Mà $\widehat{AMB}+\widehat{BMC}=180{}^\circ $ ( Kề bù )
nên $\widehat{BMC}+\widehat{CMD}=180{}^\circ $
Vậy ba điểm B, M, D thẳng hàng
Bài 2 : Cho tam giác ABC. Gọi M,N lần lượt là trung điểm của các cạnh AC, AB. Trên các tia BM, CN lần lượt lấy các điểm D và E sao cho M là trung điểm BD và N là trung điểm EC. Chứng minh ba điểm E, A, D thẳng hàng.
Xem thêm: Hướng Dẫn Tra Cứu Điểm Thi Thpt Quốc Gia 2019 Nhanh Nhất Và Chính Xác Nhất
Giải
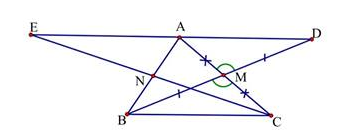
BM = DM
\<\widehat{BMC}=\widehat{DMA}\> ( đối đỉnh )
AM = CM
=>\<\Delta BMC=\Delta DMA\,\,(c.g.c)\>
=>\<\widehat{ACB}=\widehat{DAC}\> mà hai góc ở vị trí so le trong nên BC // AD (1)
Tương tự ta có : \<\Delta EAN=\Delta BNC\,\,\,(c.g.c)\> => \<\widehat{EAN}=\widehat{NBC}\>mà hai góc ở vị trí so le trong nên AE // BC (2)
Từ (1),(2) ta có : Điểm A nằm ngoài BC , theo tiên đề Ơ-clit ta có một và chỉ 1 đường thẳng song song với BC qua A => Ba điểm E, A, D song song.
Bài 3 : Cho tam giác ABC, trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Vẽ AH vuông góc BC ( H \<\in \>BC). Trên đoạn DE lấy điểm K sao cho BH = DK. Chứng minh ba điểm A, H, K thẳng hàng .
Hướng dẫn giải :
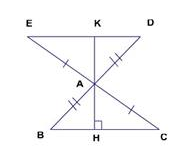
+) Chứng minh \<\Delta ABH=\Delta ADK\,\,(c.g.c)\>
=>AK // BC
Mà AH \<\bot \>BC nên ta có ba điểm K, A, H thẳng hàng .
III. Bài tập tự luyện :
Bài 1 : Cho tam giác ABC có AB = AC. Gọi M là một điểm nằm trong tam giác sao cho MB = MC. Gọi N là trung điểm của BC. Chứng minh ba điểm A, M, N thẳng hàng .
Bài 2 : Cho ba tam giác cân ABC, DBC và EBC có chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.
Bài 3 : Cho tam giác ABC, kẻ trung tuyến AM. Trên AM lấy điểm P, Q sao cho AQ = PQ = PM. Gọi E là trung điểm của AC. Chứng minh ba điểm B, P, E thẳng hàng.
Bài 4 : Cho tam giác ABC cân tại A, vẽ đường cao BH và CK cắt nhau tại I. Gọi M là trung điểm BC. Chứng minh A, I, M thẳng hàng.
Bài 5 : Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và CD. Chứng minh ba điểm M, A, N thẳng hàng .
Bài 6 : Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm E sao cho CE = BD. Kẻ DH và EK vuông góc với BC ( H và K thuộc BC). Gọi M là trung điểm HK. Chứng minh ba điểm D, M, E thẳng hàng.
Bài 7 : Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng .
Bài 8 : Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chứng minh ba điểm M, C, N thẳng hàng.
Bài viết gợi ý:1. Cộng trừ số hữu tỉ 2. Cộng trừ đa thức 3. Nghiệm của đa thức một biến 4. tổng hợp các bài toán hình học nâng cao lớp 7 5. Đơn thức đa thức 6. Bất đẳng thức trong tam giác 7. Số hữu tỉ











