40 đề thi toán vào lớp 10 chọn lọc

Lớp 1

Đề thi lớp 1

Lớp 2

Lớp 2 - liên kết tri thức

Lớp 2 - Chân trời sáng tạo

Lớp 2 - Cánh diều

Tài liệu tham khảo

Lớp 3

Lớp 3 - kết nối tri thức

Lớp 3 - Chân trời sáng sủa tạo

Lớp 3 - Cánh diều

Tài liệu tham khảo

Lớp 4

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Lớp 5

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Lớp 6

Lớp 6 - kết nối tri thức

Lớp 6 - Chân trời sáng tạo

Lớp 6 - Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 7

Lớp 7 - liên kết tri thức

Lớp 7 - Chân trời sáng tạo

Lớp 7 - Cánh diều

Sách/Vở bài xích tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 8

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 9

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 10

Lớp 10 - kết nối tri thức

Lớp 10 - Chân trời sáng sủa tạo

Lớp 10 - Cánh diều

Sách/Vở bài xích tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 11

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 12

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề và Trắc nghiệm

IT

Ngữ pháp giờ đồng hồ Anh

Lập trình Java

Phát triển web

Lập trình C, C++, Python

Cơ sở dữ liệu

Nhằm giúp chúng ta ôn luyện cùng giành được công dụng cao vào kì thi tuyển sinh vào lớp 10, vanhoanghean.com soạn tuyển tập Đề thi vào lớp 10 môn Toán (có đáp án) theo cấu trúc ra đề Trắc nghiệm - trường đoản cú luận mới. Cùng rất đó là các dạng bài xích tập hay có trong đề thi vào lớp 10 môn Toán với phương pháp giải bỏ ra tiết. Hi vọng tài liệu này sẽ giúp học sinh ôn luyện, củng cố kỹ năng và sẵn sàng tốt mang đến kì thi tuyển chọn sinh vào lớp 10 môn Toán năm 2022.

Bạn đang xem: 40 đề thi toán vào lớp 10 chọn lọc

I/ Đề thi môn Toán vào lớp 10 (không chuyên)

Bộ Đề thi vào lớp 10 môn Toán năm 2022 bao gồm đáp án (Trắc nghiệm - trường đoản cú luận)

Bộ Đề thi vào lớp 10 môn Toán năm 2022 có đáp án (Tự luận)

Bộ Đề thi vào lớp 10 môn Toán TP tp hà nội năm 2021 - 2022 bao gồm đáp án

II/ Đề thi môn Toán vào lớp 10 (chuyên)

III/ các dạng bài tập ôn thi vào lớp 10 môn Toán

Tài liệu ôn thi vào lớp 10 môn Toán

Sở giáo dục đào tạo và Đào chế tác .....

Kỳ thi tuyển sinh vào lớp 10

Đề thi môn: Toán

Năm học tập 2021 - 2022

Thời gian: 120 phút

Câu 1: (2 điểm) Rút gọn gàng biểu thức sau:

a) A=12−253+60.

b) B=4xx−3.x2−6x+9x với 0 x2−2mx+m2−m+3=0 (1), cùng với m là tham số.

a) Giải phương trình (1) cùng với m = 4.

b) Tìm các giá trị của m nhằm phương trình (1) gồm hai nghiệm với biểu thức: P=x1x2−x1−x2 đạt giá trị nhỏ dại nhất.

Câu 3: (1,5 điểm)

Tình cảm gia đình có sức khỏe phi trường. Các bạn Vì quyết đấu – Cậu bé xíu 13 tuổi qua thương ghi nhớ em trai của bản thân mình đã vượt sang một quãng đường dài 180km từ sơn La đến bệnh viện Nhi Trung ương hà nội thủ đô để thăm em. Sau thời điểm đi bằng xe đạp 7 giờ, chúng ta ấy được lên xe pháo khách và đi tiếp 1 giờ 30 phút nữa thì tới nơi. Biết gia tốc của xe khách lớn hơn vận tốc của xe đạp điện là 35 km/h. Tính gia tốc xe đạp của người tiêu dùng Chiến.

Câu 4: (3,0 điểm)

mang đến đường tròn (O) gồm hai đường kính AB và MN vuông góc cùng với nhau. Bên trên tia đối của tia MA mang điểm C khác điểm M. Kẻ MH vuông góc với BC (H thuộc BC).

a) chứng tỏ BOMH là tứ giác nội tiếp.

b) MB giảm OH trên E. Chứng tỏ ME.MH = BE.HC.

c) hotline giao điểm của đường tròn (O) với con đường tròn ngoại tiếp ∆MHC là K. Minh chứng 3 điểm C, K, E trực tiếp hàng.

Câu 5: (1,0 điểm) Giải phương trình: 5x2+27x+25−5x+1=x2−4.

 

HƯỚNG DẪN GIẢI ĐỀ SỐ 03

Câu 1:

a) A=12−253+60=36−215+215=36=6

b) cùng với 0 B=4xx−3.x2−6x+9x =2xx−3.x−32x=−2x3−x.x−3x=−2x3−x3−xx=−2

Câu 2:

1) vì đồ thị hàm số đi qua điểm M(1; –1) đề xuất a+ b = -1

đồ thị hàm số trải qua điểm N(2; 1) đề xuất 2a + b = 1

yêu thương cầu bài toán a+b=−12a+b=1⇔a=2b=−3

Vậy hàm số bắt buộc tìm là y = 2x – 3.

2)

a) với m = 4, phương trình (1) trở thành: x2−8x+15=0. Có Δ=1>0

Phương trình bao gồm hai nghệm phân biệt x1=3; x2=5;

b) Ta có: ∆" = −m2−1.m2−m+3=m2−m2+m−3=m−3.

Phương trình (1) tất cả hai nghiệm x1, x2 lúc ∆" 0 ⇔ m−3≥0⇔m≥3

Với m≥3, theo định lí Vi–ét ta có: x1+x2=2mx1.x2=m2−m+3

Theo bài ra: P=x1x2−x1−x2=x1x2−(x1+x2)

Áp va định lí Vi–ét ta được:

P=m2−m+3−2m=m2−3m+3 =m(m−3)+3

bởi m≥3 nên m(m−3)≥0 , suy ra P≥3. Vết " = " xảy ra khi m = 3.

Vậy giá bán trị nhỏ nhất của p là 3 lúc m = 3.

Câu 3:

Đổi 1 giờ 30 phút = 1,5 giờ.

Xem thêm: Trường Đại Học Kinh Tế - Thông Tin Tuyển Sinh Đại Học Kinh Tế

Gọi tốc độ xe đạp của người sử dụng Chiến là x (km/h, x > 0)

vận tốc của ô tô là x + 35 (km/h)

Quãng đường các bạn Chiến đi bằng xe đạp là: 7x (km)

Quãng đường các bạn Chiến đi bằng ô tô là: 1,5(x + 35)(km)

do tổng quãng đường bạn Chiến đi là 180km buộc phải ta gồm phương trình:

7x + 1,5(x + 35) = 180 7x + 1,5x + 52,2 = 180 8,5x = 127,5 x = 15

(thỏa mãn)

Vậy chúng ta Chiến đi bằng xe đạp với vận tốc là 15 km/h.

Câu 4:

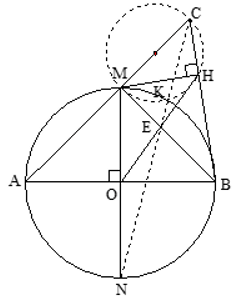
a) Ta có: MOB^=900 (do AB⊥MN) cùng MHB^=900(do MH⊥BC)

Suy ra: MOB^+MHB^=900+900=1800

=> Tứ giác BOMH nội tiếp.

b) ∆OMB vuông cân tại O phải OBM^=OMB^ (1)

Tứ giác BOMH nội tiếp buộc phải OBM^=OHM^ (cùng chắn cung OM)

và OMB^=OHB^ (cùng chắn cung OB) (2)

trường đoản cú (1) cùng (2) suy ra: OHM^=OHB^

=> HO là tia phân giác của MHB^ => MEBE=MHHB (3)

Áp dụng hệ thức lượng vào ∆BMC vuông trên M gồm MH là con đường cao

Ta có: HM2=HC.HB⇒HMHB=HCHM (4)

tự (3) và (4) suy ra: MEBE=HCHM5⇒ME.HM=BE.HC (đpcm)

c) vày MHC^=900(do MH⊥BC) phải đường tròn nước ngoài tiếp ∆MHC có đường kính là MC

⇒MKC^=900 (góc nội tiếp chắn nửa đường tròn)

MN là đường kính của mặt đường tròn (O) nên MKN^=900 (góc nội tiếp chắn nửa mặt đường tròn)

⇒MKC^+MKN^=1800

=> 3 điểm C, K, N thẳng hàng (*)

∆MHC ∽ ∆BMC (g.g) ⇒HCMH=MCBM. 

mà lại MB = BN (do ∆MBN cân tại B)

=>HCHM=MCBN, kết hợp với MEBE=HCHM (theo (5) )

Suy ra: MCBN=MEBE . Nhưng EBN^=EMC^=900 => ∆MCE ∽ ∆BNE (c.g.c)

⇒MEC^=BEN^, mà MEC^+BEC^=1800 (do 3 điểm M, E, B trực tiếp hàng)

⇒BEC^+BEN^=1800

=> 3 điểm C, E, N thẳng mặt hàng (**)

từ bỏ (*) với (**) suy ra 4 điểm C, K, E, N thẳng hàng

=> 3 điểm C, K, E thẳng mặt hàng (đpcm)

Câu 5: ĐKXĐ: x≥2

Ta có: 5x2+27x+25−5x+1=x2−4

⇔5x2+27x+25=5x+1+x2−4

⇔5x2+27x+25=x2−4+25x+25+10(x+1)(x2−4)

⇔4x2+2x+4=10x+1)(x2−4)⇔2x2+x+2=5(x+1)(x2−4) (1)

cách 1:

(1) ⇔x2−2x−44x2−13x−26=0

Giải ra được:

x=1−5(loại); x=1+5(nhận); x=13+3658 (nhận); x=13−3658 (loại)

bí quyết 2:

(1) ⇔5x2−x−2x+2=2x2−x−2+3x+2 (2)

Đặt a=x2−x+2; b=x+2 (a≥0; b≥0)

lúc đó, phương trình (2) trở thành:

5ab=2a2+3b2⇔2a2−5ab+3b2=0⇔a−b2a−3b=0⇔a=b2a=3b (*)

 – với a = b thì x2−x−2=x+2⇔x2−2x−4⇔x=1−5(ktm)x=1+5(tm)

 – cùng với 2a = 3b thì 2x2−x−2=3x+2⇔4x2−13x−26=0⇔x=13+3658 (tm)x=13−3658 (ktm)

Vậy phương trình đang cho tất cả hai nghiệm: x=1+5 và x=13+3658 .

Sở giáo dục và đào tạo và Đào tạo .....

Kỳ thi tuyển chọn sinh vào lớp 10

Đề thi môn: Toán

Năm học 2021 - 2022

Thời gian: 120 phút

Sở giáo dục đào tạo và Đào chế tác .....

Kỳ thi tuyển chọn sinh vào lớp 10

Đề thi môn: Toán

Năm học tập 2021 - 2022

Thời gian: 120 phút

Phần I. Trắc nghiệm (2 điểm)

Câu 1: Điều kiện khẳng định của biểu thức

là:

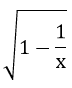
A.x ≠ 0 B.x ≥ 1 C.x ≥ 1 hoặc x 2 và đường thẳng (d) y =

+ 3

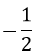
A. (2; 2)B. ( 2; 2) và (0; 0)

C.(-3; ) D.(2; 2) với (-3; )

Câu 5: quý giá của k để phương trình x2 + 3x + 2k = 0 gồm 2 nghiệm trái vệt là:

A. K > 0B. K 2 D. K (2 điểm)

1) Thu gọn biểu thức

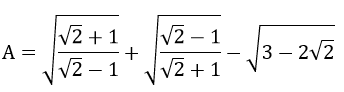
2) giải phương trình và hệ phương trình sau:

a) 3x2 + 5x - 8 = 0

b) (x2 + 5)2 = 3(x2 + 5) + 4

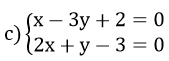
Bài 2: (1,5 điểm) Trong khía cạnh phẳng tọa độ Oxy cho Parabol (P) : y = x2 và đường thẳng (d) :

y = 2mx – 2m + 1

a) với m = -1 , hãy vẽ 2 vật thị hàm số trên cùng một hệ trục tọa độ

b) kiếm tìm m nhằm (d) với (P) cắt nhau trên 2 điểm tách biệt : A (x1; y1 );B(x2; y2) làm sao cho tổng những tung độ của nhị giao điểm bởi 2 .

Bài 3: (1 điểm) Rút gọn biểu thức sau:

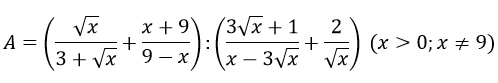
Tìm x để A (3,5 điểm) cho đường tròn (O) bao gồm dây cung CD cố gắng định. điện thoại tư vấn M là điểm nằm ở trung tâm cung bé dại CD. Đường kính MN của con đường tròn (O) cắt dây CD tại I. Rước điểm E ngẫu nhiên trên cung bự CD, (E khác C,D,N); ME giảm CD tại K. Những đường thẳng NE và CD cắt nhau tại P.

a) chứng tỏ rằng :Tứ giác IKEN nội tiếp

b) bệnh minh: EI.MN = NK.ME

c) NK giảm MP trên Q. Bệnh minh: IK là phân giác của góc EIQ

d) tự C vẽ con đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung khủng CD (E không giống C, D, N) thì H luôn chạy bên trên một đường ráng định.

Phần I. Trắc nghiệm

1.C	2.D	3.A	4.D
5.B	6.A	7.D	8.B

Phần II. Tự luận

Bài 1:

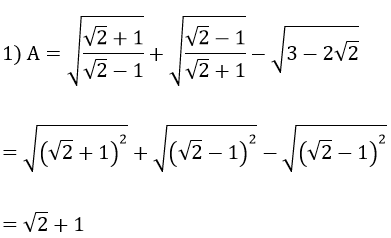
2) a) 3x2 + 5x - 8 = 0

Δ = 52 - 4.3.(-8) = 121 => √Δ = 11

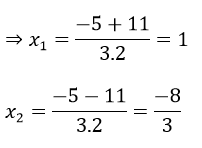
Vậy phương trình sẽ cho gồm tập nghiệm là S =

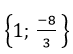
b) (x2 + 3)2 = 3(x2 + 3) + 4

Đặt x2 + 3 = t (t ≥ 3), phương trình vẫn cho biến

t2 - 3t - 4 = 0

Δ = 32 - 4.(-4) = 25> 0

Phương trình tất cả 2 nghiệm phân biệt :

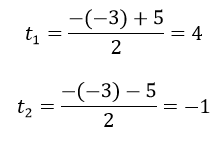
Do t ≥ 3 phải t = 4

Với t = 4, ta có: x2 + 3 = 4 ⇔ x2 = 1 ⇔ x = ±1

Vậy phương trình đã cho tất cả 2 nghiệm x = ± 1

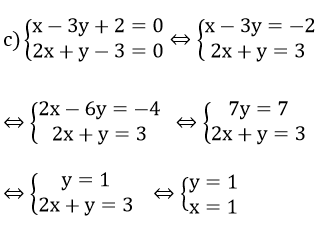
Bài 2:

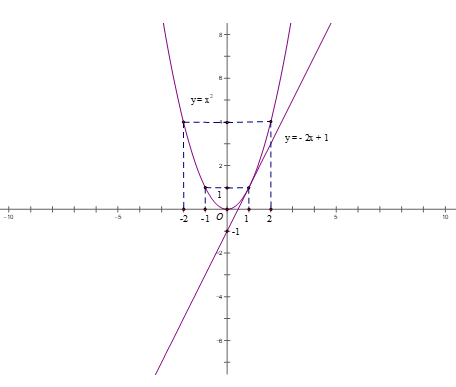
Trong mặt phẳng tọa độ Oxy mang lại Parabol (P) : y = x2 và mặt đường thẳng (d) :

y = 2mx – 2m + 1

a) với m = 1; (d): y = 2x – 1

Bảng quý giá

x	0	1
y = 2x – 1	-1	1

(P) : y = x2

Bảng giá chỉ trị

x	-2	-1	0	1	2
y = x2	4	1	0	1	4

Đồ thị hàm số y = x2 là đường parabol nằm bên trên trục hoành, nhận Oy làm cho trục đối xứng với nhận điểm O(0; 0) là đỉnh cùng điểm thấp nhất

b) mang đến Parabol (P) : y = x2 và đường thẳng (d) :

y = 2mx – 2m + 1

Phương trình hoành độ giao điểm của (P) và (d) là:

x2 = 2mx - 2m + 1

⇔ x2 - 2mx + 2m - 1 = 0

Δ" = mét vuông - (2m - 1)=(m - 1)2

(d) và (P) cắt nhau tại 2 điểm riêng biệt khi và chỉ còn khi phương trình hoành độ giao điểm có 2 nghiệm sáng tỏ

⇔ Δ" > 0 ⇔ (m - 1)2 > 0 ⇔ m ≠ 1

Khi đó (d) giảm (P) tại 2 điểm A(x1, 2mx1 – 2m + 1) ; B ( x2, 2mx2 – 2m + 1)

Theo định lí Vi-et ta có: x1 + x2 = 2m

Từ giả thiết đề bài, tổng những tung độ giao điểm bằng 2 đề xuất ta có:

2mx1 – 2m + 1 + 2mx2 – 2m + 1 = 2

⇔ 2m (x1 + x2) – 4m + 2 = 2

⇔ 4m2 - 4m = 0 ⇔ 4m(m - 1) = 0

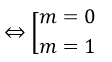
Đối chiếu với điều kiện m ≠ 1, thì m = 0 thỏa mãn.

Bài 3:

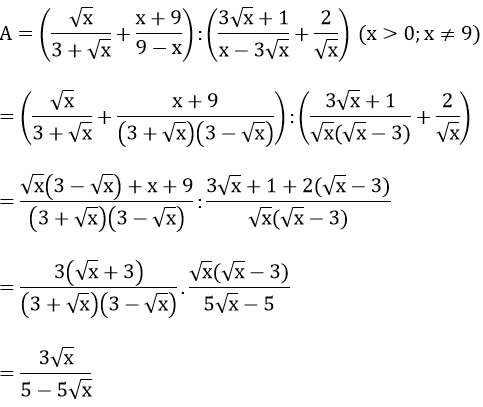
A > 0 ⇔

> 0 ⇔ 5 - 5√x > 0 ⇔ √x 0 khi 0 ∠KIN = 90o

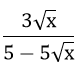
Xét tứ giác IKEN có:

∠KIN = 90o

∠KEN = 90o (góc nội tiếp chắn nửa đường tròn)

=> ∠KIN + ∠KEN = 180o

=> Tứ giác IKEN là tứ giác nội tiếp

b) Xét ΔMEI cùng ΔMNK có:

∠NME là góc chung

∠IEM = ∠MNK ( 2 góc nội tiếp thuộc chắn cung IK)

=> ΔMEI ∼ ΔMNK (g.g)

=>EI.MN = NK.ME

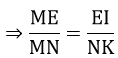
c) Xét tam giác MNP có:

ME ⊥ NP; PI ⊥ MN

ME giao PI tại K

=> K là trực tâm của tam giác MNP

=> ∠NQP = 90o

Xét tứ giác NIQP có:

∠NQP = 90o

∠NIP = 90o

=> 2 đỉnh Q, I cùng chú ý cạnh NP bên dưới 1 góc bằng nhau

=> tứ giác NIQP là tứ giác nội tiếp

=> ∠QIP = ∠QNP (2 góc nội tiếp cùng chắn cung PQ)(1)

Mặt khác IKEN là tứ giác nội tiếp

=> ∠KIE = ∠KNE (2 góc nội tiếp thuộc chắn cung KE)(2)

Từ (1) với (2)

=> ∠QIP = ∠KIE

=> IE là tia phân giác của ∠QIE

d) Ta có:

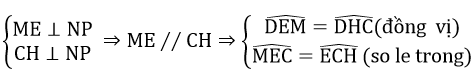
Mà ∠DEM = ∠MEC (2 góc nội tiếp chắn 2 cung bởi nhau)

=> ∠EHC = ∠ECH => ΔEHC cân nặng tại E

=> EN là mặt đường trung trực của CH

Xét đường tròn (O) có: Đường kính OM vuông góc cùng với dây CD tại I

=> NI là đường trung trực của CD => NC = ND

EN là mặt đường trung trực của CH => NC = NH

=> N là trung tâm đường tròn nước ngoài tiếp tam giác DCH

=> H ∈ (N, NC)

Mà N, C cố định và thắt chặt => H thuộc đường tròn cố định

Sở giáo dục và đào tạo và Đào sản xuất .....

Kỳ thi tuyển chọn sinh vào lớp 10

Đề thi môn: Toán

Năm học 2021 - 2022

Thời gian: 120 phút

Bài 1 : ( 1,5 điểm)

1) Rút gọn biểu thức sau:

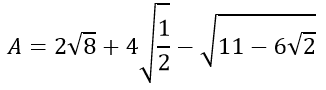
2) đến biểu thức

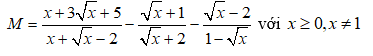
a) Rút gọn gàng biểu thức M.

b) Tìm các giá trị nguyên của x để giá trị tương xứng của M nguyên.

Bài 2 : ( 1,5 điểm)

1) tra cứu m để hai phương trình sau có ít nhất một nghiệm chung:

2x2 – (3m + 2)x + 12 = 0

4x2 – (9m – 2)x + 36 = 0

2) Tìm hệ số a, b của đường thẳng y = ax + b biết con đường thẳng trên đi qua hai điểm là

(1; -1) cùng (3; 5)

Bài 3 : ( 2,5 điểm)

1) đến Phương trình :x2 + (m - 1) x + 5m - 6 = 0

a) giải phương trình khi m = - 1

b) kiếm tìm m nhằm 2 nghiệm x1 và x2 thỏa mãn nhu cầu hệ thức: 4x1 + 3x2 = 1

2) Giải vấn đề sau bằng phương pháp lập phương trình hoặc hệ phương trình

Một công ty vận tải đường bộ điều một số xe tải để chở 90 tấn hàng. Khi tới kho sản phẩm thì có 2 xe pháo bị hỏng cần để chở không còn số hàng thì mỗi xe sót lại phải chở thêm 0,5 tấn so với dự tính ban đầu. Hỏi số xe pháo được điều cho chở sản phẩm là bao nhiêu xe? Biết rằng khối lượng hàng chở làm việc mỗi xe cộ là như nhau.

Bài 4 : ( 3,5 điểm)

1) mang lại (O; R), dây BC cố định và thắt chặt không đi qua tâm O, A là điểm bất kì bên trên cung bự BC. Ba đường cao AD, BE, CF của tam giác ABC giảm nhau tại H.

a) chứng tỏ tứ giác HDBF, BCEF nội tiếp

b) K là điểm đối xứng của A qua O. Chứng minh HK đi qua trung điểm của BC

c) Gỉa sử ∠BAC = 60o. Chứng tỏ Δ AHO cân

2) Một hình chữ nhật tất cả chiều nhiều năm 3 cm, chiều rộng bởi 2 cm, con quay hình chữ nhật này một vòng quanh chiều dài của chính nó được một hình trụ. Tính diện tích s toàn phần của hình trụ.

Bài 5 : ( 1 điểm)

1) mang đến a, b là 2 số thực làm sao cho a3 + b3 = 2. Chứng minh:

0 √x - 1 ∈ Ư (2)

√x - 1 ∈ ±1; ±2

Ta gồm bảng sau:

√x-1	- 2	-1	1	2
√x	-1	0	2	3
x	Không vĩnh cửu x	0	4	9

Vậy cùng với x = 0; 4; 9 thì M nhận quý hiếm nguyên.

Bài 2 :

1)

2x2 – (3m + 2)x + 12 = 0

4x2 – (9m – 2)x + 36 = 0

Đặt y = x2,khi đó ta có:

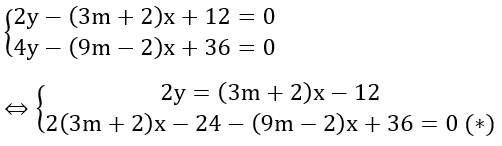
Giải (*):

(6 - 3m)x = -12

Phương trình (*) tất cả nghiệm 6 - 3m ≠ 0 m ≠ 2

Khi đó, phương trình tất cả nghiệm:

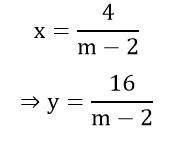
Theo giải pháp đặt, ta có: y = x2

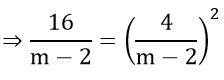
=>16(m-2) = 16

m = 3

Thay m= 3 vào 2 phương trình ban đầu,ta có:

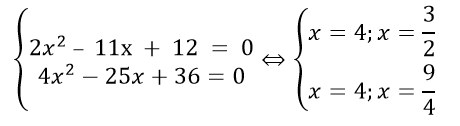
Vậy khi m =3 thì nhị phương trình trên có nghiệm chung và nghiệm bình thường là 4

2) Tìm thông số a, b của mặt đường thẳng y = ax + b biết đường thẳng trên đi qua hai điểm là

(1; -1) cùng (3; 5)

Đường trực tiếp y = ax + b đi qua hai điểm (1; -1) và (3; 5) yêu cầu ta có:

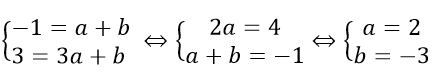
Vậy con đường thẳng yêu cầu tìm là y = 2x – 3

Bài 3 :

1) mang đến Phương trình : x2 + (m - 1)x + 5m - 6 = 0

a) lúc m = -1, phương trình trở thành:

x2 - 2x - 11 = 0

Δ" = 1 + 11=12 => √(Δ") = 2√3

Phương trình tất cả nghiệm:

x1 = 1 + 2√3

x2 = 1 - 2√3

Vậy hệ phương trình có tập nghiệm là:

S =1 + 2√3; 1 - 2√3

b)

x2 + (m - 1)x + 5m - 6 = 0

Ta có:

Δ = (m - 1)2 - 4(5m - 6)

Δ = mét vuông - 2m + 1 - 20m + 24 = mét vuông - 22m + 25

Phương trình có hai nghiệm ⇔ Δ ≥ 0 ⇔ m2 - 22m + 25 ≥ 0,(*)

Theo hệ thức Vi-ét ta có:

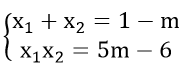
Theo đề bài xích ta có:

4x1 + 3x2 =1 ⇔ x1 + 3(x1 + x2 ) = 1

⇔ x1 + 3(1 - m) = 1

⇔ x1= 3m - 2

=> x2 = 1 - m - x1 = 1 - m - (3m - 2) = 3 - 4m

Do kia ta có:

(3m - 2)(3 - 4m) = 5m - 6

⇔ 9m - 12m2 - 6 + 8m = 5m - 6

⇔ - 12m2 + 12m = 0

⇔ -12m(m - 1) = 0

⇔

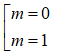
Thay m = 0 vào (*) thấy thảo mãn

Thay m = 1 vào (*) thấy thảo mãn

Vậy có hai cực hiếm của m thỏa mãn bài toán là m = 0 cùng m = 1.

2)

Gọi con số xe được điều mang đến là x (xe) (x > 0; x ∈ N)

=>Khối lượng mặt hàng mỗi xe pháo chở là:

(tấn)

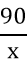
Do tất cả 2 xe cộ nghỉ đề xuất mỗi xe còn sót lại phải chở thêm 0,5 tấn so với dự định nên từng xe bắt buộc chở:

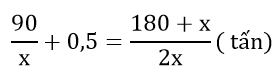
Khi đó ta gồm phương trình:

.(x-2)=90

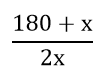
=>(180 + x)(x - 2) = 180x

x2 - 2x - 360 = 0

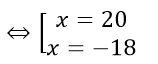
Vậy số xe được điều mang lại là trăng tròn xe

Bài 4 :

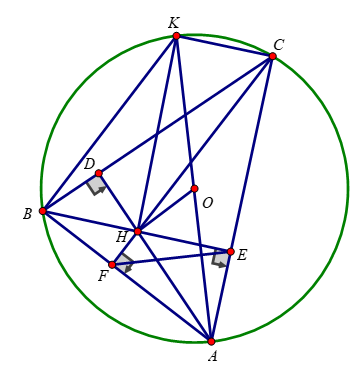
a) Xét tứ giác BDHF có:

∠BDH = 90o (AD là con đường cao)

∠BFH = 90o (CF là con đường cao)

=>∠BDH + ∠BFH = 180o

=> Tứ giác BDHF là tứ giác nội tiếp

Xét tứ giác BCEF có:

∠BFC = 90o (CF là con đường cao)

∠BEC = 90o (BE là mặt đường cao)

=> 2 đỉnh E và F cùng nhìn cạnh BC dưới 1 góc vuông

=> Tứ giác BCEF là tứ giác nội tiếp

b) Ta có:

∠KBA) = 90o (góc nội tiếp chắn nửa con đường tròn)

=>KB⊥AB

Mà CH⊥AB (CH là đường cao)

=> KB // CH

Tương tự:

∠KCA) = 90o (góc nội tiếp chắn nửa đường tròn)

=>KC⊥AC

BH⊥AC (BH là mặt đường cao)

=> HB // chồng

Xét tứ giác BKCF có:

KB // CH

HB // CK

=> Tứ giác BKCH là hình bình hành

=> nhì đường chéo cánh BC với KH giảm nhau trên trung điểm mỗi đường

=> HK đi qua trung điểm của BC

c) hotline M là trung điểm của BC

Xét tam giác AHK có:

O là trung điểm của AK

M là trung điểm của BC

=> OM là con đường trung bình của tam giác AHK

=> OM = AH (1)

ΔBOC cân nặng tại O có OM là trung tuyến đường

=> OM là tia phân giác của ∠BOC

=> ∠MOC = ∠BAC = 60o (= ∠BOC )

Xét tam giác MOC vuông tại M có:

OM = OC.cos⁡(MOC) = OC.cos⁡60o= OC = OA (2)

Từ (1) và (2) => OA = AH => ΔOAH cân tại A

2)

Quay hình chữ nhật vòng quanh chiều dài được một hình tròn có bán kính đáy là R= 2 cm, chiều cao là h = 3 cm